miércoles, 10 de octubre de 2012
Geometría Analítica
Areli Ramirez Saldana
Martha Reyna Martinez
“LA LINEA RECTA”
3,k
12 de octubre del 2012
INVESTIGACIÓN 2º PARCIAL
Angulo de inclinación y pendiente de una recta:
Consideramos como (ángulo de inclinación) a aquel ángulo que se pueda presentar entre un segmento plano (Horizonte) y otro segmento distante.
Es necesario conocer la pendiente de una vía con respecto a otra para evitar una mala construcción del mismo.
Pues podría generarse una situación de una mala edificiación lo cual repercutiría en unos cuartos mal construidos. Todo estos detalles muy importantes para poder llevar un trabajo adelante.
Pues podría generarse una situación de una mala edificiación lo cual repercutiría en unos cuartos mal construidos. Todo estos detalles muy importantes para poder llevar un trabajo adelante.
Esta misma analogía podría ser ubicada en la comodidad del hogar, en las esquinas de las habitaciones. Si suponemos querer tener una habitación en la que la edificación de los cuartos cuadre es necesario, de cierta manera conocer a que ángulos inclinación estan dictadas las paredes.
La pendiente de una recta en un sistema de representación de un plano cartesiano , suele ser representado por la letra , y es definido como el cambio o diferencia en el eje Y dividido por el respectivo cambio en el eje X, entre 2 puntos de la recta. En la siguienteecuación se describe: toda recta que no sea horizontal, tiene que cortar al eje "x". se dice que si una recta corta al eje X, la inclinación de la recta se define como el ángulo positivo menor de 180°.
Una recta horizontal tiene pendiente igual a 0 (cero). Cuanto menor sea el valor de la pendiente, menor inclinación tendrá la recta; por ejemplo, una recta que se eleve un ángulo de 45° con respecto al eje X tiene una pendiente m = +1, y una recta que caiga 30° tiene pendiente m = -0,5. La pendiente de una recta vertical no está definida, o se dice que es infinita.
Condiciones de paralelismo y perpendicularidad :
Si las pendientes de dos rectas son iguales, entonces ambas rectas son paralelas entre sí.
Si el producto de las pendientes de dos rectas es igual a -1, entonces ambas rectas son perpendiculares entre sí.
El problema de saber si dos o más rectas son perpendiculares o paralelas está en conocer cuales son sus pendientes. La pendiente de una recta m = (y2-y1)/(x2-x1), o sea que conociendo dos puntos cualesquiera de la recta puedes saber su pendiente m y así saber si es paralela o perpendicular a otra recta.
Paralelismo
Dos rectas son paralelas si tienen la misma dirección y ésto ocurre cuando sus vectores de dirección son iguales o proporcionales.
Dos rectas son paralelas si tienen la misma dirección y ésto ocurre cuando sus vectores de dirección son iguales o proporcionales.
Dos rectas son paralelas si y sólo si sus pendientes coinciden: .
Perpendicularidad
Dos rectas son perpendiculares si sus vectores de dirección son ortogonales, o lo que es lo mismo, si el producto escalar de sus vectores de dirección es cero. Traduciendo ésto a coordenadas: Dos rectas con vectores de dirección y son perpendiculares
Determinación de la ecuación de una recta:
La ecuación explícita de una recta tiene la forma y=mx+n donde m es la pendiente de la recta y n el término independiente. En el siguiente ejercicio te proponemos, que bien conociendo la pendiente m y un punto P por el que pasa determines m y n, o bien conociendo dos puntos determinar m y n. Recuerda que si tienes dos puntos puedes sustituirlos en la ecuación y plantear un sistema con dos ecuaciones y dos incógnitas (m y n).-Sabiendo un punto y su pendiente.
La forma mas fácil para encontrar la ecuación de una recta es conociendo uno de sus puntos P(x0,y0) y su pendiente m.
Basta recurrir a la expresión punto-pendiente y-yo=m(x-x0).
-Conociendo un punto y su dirección.
Ecuación de una recta cuando conocemos uno de sus puntos P(x0,y0) y su dirección
La dirección del vector nos da la pendiente de la recta lo que nos lleva al caso anterior.
-Conociendo dos de sus puntos.
Ecuación de una recta cuando conocemos dos de sus puntos P(x0,y0)y Q (x1,y1)
El vector es un vector direccional de la recta y tiene de componentes (x1-x0,y1-y0) y su pendiente será .
Con su pendiente y la intersección con el eje OY (ordenada en el origen).
Si se conoce su pendiente m y su coordenada en el origen (0,n), basta sustituirlas en la forma punto-pendiente y-n=mx ? y=mx+n.
Distintas formas de la ecuación de la recta:
-Ecuación de la línea recta que pasa por un punto A(X1,Y1) y la pendiente conocida m .
- Conociendo otro punto cualesquiera de la recta P(X,Y) como se indica en la figura:
Apliquemos la fórmula de la pendiente:
Y - Y1 = m(X - X1) Ecuación de la Recta de Punto y Pendiente.
Ecuación de la Línea Recta con Pendiente y Ordenada en el Origen.
Sea una recta con pendiente m que intersecta al eje y en el punto (O,b), siendo b la ordenada al origen y sea P(X,Y) otro punto de la recta como se indica en la figura:
- Conociendo otro punto cualesquiera de la recta P(X,Y) como se indica en la figura:
Apliquemos la fórmula de la pendiente:
Y - Y1 = m(X - X1) Ecuación de la Recta de Punto y Pendiente.
Ecuación de la Línea Recta con Pendiente y Ordenada en el Origen.
Sea una recta con pendiente m que intersecta al eje y en el punto (O,b), siendo b la ordenada al origen y sea P(X,Y) otro punto de la recta como se indica en la figura:
Aplicamos la fórmula de la pendiente:
Despejando y tendremos Ecuación de la Recta de la Pendiente-Ordenada en el Origen (intersección).y = mx + b
Ecuación de la recta en forma normal:
Los puntos A y X de la recta r determinan el vector:
= (x - a1, y - a2)
El vector
es un vector unitario y perpendicular a r.
Los puntos A y X de la recta r determinan el vector:
= (x - a1, y - a2)El vector
es un vector unitario y perpendicular a r.
Si las componentes del vector director de r son (-B, A), las componentes de su vector perpendicular correspondiente son: (A, B).
Por tanto las componentes del vector unitario y perpendicular serán:
Como y son perpendiculares, su producto escalar es cero:
Como
y son perpendiculares, su producto escalar es cero:
Si en la ecuación general sustituimos las coordenadas del punto A, obtenemos:
Ejemplo:La ecuación normal de la recta r≡12x-5+260 es:
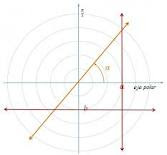
Forma polar de la ecuación de una recta;
Se le llama ecuación polar a la ecuación que define una curva expresada en coordenadas polares.
Se pueden deducir diferentes formas de simetría de la ecuación de una función polar . Si(−θ) = (θ) la curva será simétrica respecto al eje horizontal (0°/180°), si (180°−θ) = (θ) será simétrica respecto al eje vertical (90°/ 270°), y si (θ−α°) = (θ) será simétrico rotacionalmente α° en sentido horario respecto al polo.
Debido a la naturaleza circular del sistema de coordenadas polar, muchas curvas se pueden describir con una simple ecuación polar, mientras que en su forma cartesiana sería mucho más intrincado. Algunas de las curvas más conocidas son la rosa polar, la espiral de Arquímedes, la lemniscata, el caracol de Pascal y la cardioide.
Se pueden deducir diferentes formas de simetría de la ecuación de una función polar . Si(−θ) = (θ) la curva será simétrica respecto al eje horizontal (0°/180°), si (180°−θ) = (θ) será simétrica respecto al eje vertical (90°/ 270°), y si (θ−α°) = (θ) será simétrico rotacionalmente α° en sentido horario respecto al polo.
Debido a la naturaleza circular del sistema de coordenadas polar, muchas curvas se pueden describir con una simple ecuación polar, mientras que en su forma cartesiana sería mucho más intrincado. Algunas de las curvas más conocidas son la rosa polar, la espiral de Arquímedes, la lemniscata, el caracol de Pascal y la cardioide.
Para los apartados siguientes se entiende que el círculo, la línea y la rosa polar no tienen restricciones en el dominio y rango de la curva.
Las líneas radiales (aquellas que atraviesan el polo) se representan mediante la ecuación
donde f es el ángulo de elevación de la línea, esto es, f = arctan donde es la pendiente de la línea en el sistema de coordenadas cartesianas. La línea no radial que cruza la línea radial ? = f perpendicularmente al punto ( 0, f) tiene la ecuación
donde f es el ángulo de elevación de la línea, esto es, f = arctan donde es la pendiente de la línea en el sistema de coordenadas cartesianas. La línea no radial que cruza la línea radial ? = f perpendicularmente al punto ( 0, f) tiene la ecuación
Angulo de intersección entre dos rectas :
Se define el ANGULO entrel1 y l2 como
el ángulo positivo obtenido al rotar la rectal2 hacia l1 .
En este caso, el ángulo entre l1 y l2 viene dado por:
b1 = q1 - q2 (1)
El propósito ahora es establecer una relación entre las pendientes de dos rectas y el ángulo entre ellas.De la igualdad (1) se tiene:
tan b1 = tan (q1 - q2)
(2)También,cot b1 = cot (q1 - q2)
(3)Puesto que m1=tan q1 y m2=tan q2 , entonces las igualdades (2) y (3) podemos escribirlas en la forma:tan b1
, (2)’y cot b1
, (3)’Las ecuaciones (2)’ y (3)’ expresan la tangente y la cotangente del ángulo b1, entre las rectas l1 y l2 en términos de sus pendientes y por medio de ellas se pueden establecer criterios de perpendicularidad y paralelismo entre rectas, como la afirma el siguiente teorema.
Se define el ANGULO entrel1 y l2 como el ángulo positivo obtenido al rotar la rectal 2 hacia l1 . En este caso, el ángulo entre l1 y l2 viene dado por:
b1 = q1 - q2 (1).
El propósito ahora es establecer una relación entre las pendientes de dos rectas y el ángulo entre ellas.
De la igualdad (1) se tiene:
tan b1 = tan (q1 - q2 (2)
También,
cot b1 = cot (q1 - q2)(3)
Puesto que m1=tan q1 y m2=tan q2 , entonces las igualdades (2) y (3) podemos escribirlas en la forma:
tan b1 (2)’
y cot b1 , (3)’
Las ecuaciones (2)’ y (3)’ expresan la tangente y la cotangente del ángulo b1, entre las rectas l1 y l2 en términos de sus pendientes y por medio de ellas se pueden establecer criterios de perpendicularidad y paralelismo entre rectas, como la afirma el siguiente teorema.
b1 = q1 - q2 (1).
El propósito ahora es establecer una relación entre las pendientes de dos rectas y el ángulo entre ellas.
De la igualdad (1) se tiene:
tan b1 = tan (q1 - q2 (2)
También,
cot b1 = cot (q1 - q2)(3)
Puesto que m1=tan q1 y m2=tan q2 , entonces las igualdades (2) y (3) podemos escribirlas en la forma:
tan b1 (2)’
y cot b1 , (3)’
Las ecuaciones (2)’ y (3)’ expresan la tangente y la cotangente del ángulo b1, entre las rectas l1 y l2 en términos de sus pendientes y por medio de ellas se pueden establecer criterios de perpendicularidad y paralelismo entre rectas, como la afirma el siguiente teorema.
Familia de Rectas:
La totalidad de las rectas que satisfacen una única condición geométrica se llama familia o haz de rectas, ésta definición es útil para hallar la ecuación de una recta en particular. La familia de rectas se clasifica en tres grupos los cuales son:
FAMILIAS DE RECTAS PARALELAS A UNA RECTA DADA.
Si la ecuación de la recta dada es Ax+By+C=0 y su pendiente es m=-A/B, entonces el conjunto de rectas L1 y que son paralelas a L2 tendrán por ecuación y=mx+b, por el criterio de paralelismo.
Y=-A/Bx+b entonces Ax+By+Bb
Si sustituimos la cantidad constante B por el parámetro K tendremos la ecuación de la familia de rectas paralelas a L1
L1: Ax+By+K=0FAMILIA DE RECTAS PERPENDICULARES A UNA RECTA DADA.
Si conocemos la recta L1:Ax+By+C=0 con pendiente m=-A/B y si y=mx+b es cualquiera de las rectas, L1 entonces por el criterio de perpendicularidad su ecuación será de la forma:
Y=B/Ax+b entonces L1=Bx-Ay+Ab=0
Si sustituimos por el producto Ab por el parámetro K obtenemos:
L1:Bx-Ay+K=0
FAMILIA DE RECTAS QUE PASAN POR LA INTERSECCIÓN DE DOS RECTAS.
FAMILIA DE RECTAS QUE PASAN POR LA INTERSECCIÓN DE DOS RECTAS.
El conjunto de rectas pueden ser 1,2,3……..n, que pasan por un punto se la llama también familia de rectas con centro P.
Si:
L1:Ax1+By1+C1 Y L2:A2x+B2y+C2=0
Son las rectas dadas que cortan en el centro P, la ecuación:
L1: α(A1x+B1y+C)+β(A2x+B2y+C2)=0
Multiplicando a la primera recta por α y a la segunda recta por β y a este resultado lo dividimos por α y si suponemos que β/α=K tendremos:
A1x+B1y+C1+K(A2x+B2y+C2)=0
Por medio de esta ecuación se puede determinar cualquier recta de la familia con centro P. El parámetro K es una constante para cada miembro de la familia que varía de recta en recta
FAMILIAS DE RECTAS PARALELAS A UNA RECTA DADA.
Si la ecuación de la recta dada es Ax+By+C=0 y su pendiente es m=-A/B, entonces el conjunto de rectas L1 y que son paralelas a L2 tendrán por ecuación y=mx+b, por el criterio de paralelismo.
Y=-A/Bx+b entonces Ax+By+Bb
Si sustituimos la cantidad constante B por el parámetro K tendremos la ecuación de la familia de rectas paralelas a L1
L1: Ax+By+K=0
FAMILIA DE RECTAS PERPENDICULARES A UNA RECTA DADA.
Si conocemos la recta L1:Ax+By+C=0 con pendiente m=-A/B y si y=mx+b es cualquiera de las rectas, L1 entonces por el criterio de perpendicularidad su ecuación será de la forma:
Y=B/Ax+b entonces L1=Bx-Ay+Ab=0
Si sustituimos por el producto Ab por el parámetro K obtenemos:
L1:Bx-Ay+K=0
FAMILIA DE RECTAS QUE PASAN POR LA INTERSECCIÓN DE DOS RECTAS.
El conjunto de rectas pueden ser 1,2,3……..n, que pasan por un punto se la llama también familia de rectas con centro P.
Si:
L1:Ax1+By1+C1 Y L2:A2x+B2y+C2=0
Son las rectas dadas que cortan en el centro P, la ecuación:
L1: a(A1x+B1y+C)+ß(A2x+B2y+C2)=0
Multiplicando a la primera recta por a y a la segunda recta por ß y a este resultado lo dividimos por a y si suponemos que ß/a=K tendremos:
A1x+B1y+C1+K(A2x+B2y+C2)=0
Por medio de esta ecuación se puede determinar cualquier recta de la familia con centro P. El parámetro K es una constante para cada miembro de la familia que varía de recta en recta.
Si la ecuación de la recta dada es Ax+By+C=0 y su pendiente es m=-A/B, entonces el conjunto de rectas L1 y que son paralelas a L2 tendrán por ecuación y=mx+b, por el criterio de paralelismo.
Y=-A/Bx+b entonces Ax+By+Bb
Si sustituimos la cantidad constante B por el parámetro K tendremos la ecuación de la familia de rectas paralelas a L1
L1: Ax+By+K=0
FAMILIA DE RECTAS PERPENDICULARES A UNA RECTA DADA.
Si conocemos la recta L1:Ax+By+C=0 con pendiente m=-A/B y si y=mx+b es cualquiera de las rectas, L1 entonces por el criterio de perpendicularidad su ecuación será de la forma:
Y=B/Ax+b entonces L1=Bx-Ay+Ab=0
Si sustituimos por el producto Ab por el parámetro K obtenemos:
L1:Bx-Ay+K=0
FAMILIA DE RECTAS QUE PASAN POR LA INTERSECCIÓN DE DOS RECTAS.
El conjunto de rectas pueden ser 1,2,3……..n, que pasan por un punto se la llama también familia de rectas con centro P.
Si:
L1:Ax1+By1+C1 Y L2:A2x+B2y+C2=0
Son las rectas dadas que cortan en el centro P, la ecuación:
L1: a(A1x+B1y+C)+ß(A2x+B2y+C2)=0
Multiplicando a la primera recta por a y a la segunda recta por ß y a este resultado lo dividimos por a y si suponemos que ß/a=K tendremos:
A1x+B1y+C1+K(A2x+B2y+C2)=0
Por medio de esta ecuación se puede determinar cualquier recta de la familia con centro P. El parámetro K es una constante para cada miembro de la familia que varía de recta en recta.
APLICACIONES DE LA FORMA NORMAL DE LA
ECUACIÓN DE LA RECTA:
La recta L queda determinada por la longitud de su perpendicular trazada desde el origen y el ángulo
positivo W que la perpendicular forma con el eje de las x. La perpendicular OA a la recta L, representada
por P, se considera siempre positiva por ser una distancia. EI ángulo W engendrado por OA varia de
0°= W < 360°.
Si damos valores a p y W, la recta L trazada por A(x1
, y,) queda determinada por la ecuación de la recta en
su forma normal que se obtiene en la forma siguiente:
Observando la figura anterior, tenemos:
cos w = X1/p
sen w = Y1/p
Despejamos: Despejamos:
x1 = p cos w y1 = p sen w
Sustituimos los dos valores anteriores en A = (x1 , y1), con lo cual obtenemos las coordenadas del punto A,
que son: A = (p cos W, p sen w)
Par su parte, la pendiente m de OA es: m =tan w
Como la recta L es perpendicular a la recta GA, sus pendientes están relacionadas con; m1= -1/m2
es decir, la recíproca con signo cambiado. Como ya sabemos que la pendiente de OA es tan w, la inversa
de esta función con signo cambiado de la recta L perpendicular a GA es: -cot w de donde, m =-cot w = COSW/SINW
positivo W que la perpendicular forma con el eje de las x. La perpendicular OA a la recta L, representada
por P, se considera siempre positiva por ser una distancia. EI ángulo W engendrado por OA varia de
0°= W < 360°.
Si damos valores a p y W, la recta L trazada por A(x1
, y,) queda determinada por la ecuación de la recta en
su forma normal que se obtiene en la forma siguiente:
Observando la figura anterior, tenemos:
cos w = X1/p
sen w = Y1/p
Despejamos: Despejamos:
x1 = p cos w y1 = p sen w
Sustituimos los dos valores anteriores en A = (x1 , y1), con lo cual obtenemos las coordenadas del punto A,
que son: A = (p cos W, p sen w)
Par su parte, la pendiente m de OA es: m =tan w
Como la recta L es perpendicular a la recta GA, sus pendientes están relacionadas con; m1= -1/m2
es decir, la recíproca con signo cambiado. Como ya sabemos que la pendiente de OA es tan w, la inversa
de esta función con signo cambiado de la recta L perpendicular a GA es: -cot w de donde, m =-cot w = COSW/SINW
Rectas y puntos notables de un triángulo.
Las rectas y puntos notables de un triángulo son:
las mediatrices, , que se cortan en un punto llamado circuncentro ,centro de la circunferencia circunscrita al triángulo;
las medianas, , que se cortan en el baricentro, , centro de gravedad del triángulo;
las bisectrices, , que se cortan en el incentro , centro de la circunferencia inscrita del triángulo;
las alturas, , que se cortan en el orto centro, .
Las mediatrices
Las mediatrices de un triángulo acutángulo se cortarán siempre en un punto interior del triángulo, luego su circuncentro será interior al triángulo.
En el caso del triángulo rectángulo vemos que el circuncentro coincide con el punto medio de la hipotenusa
En el caso de un triángulo obtusángulo, el circuncentro es exterior al triángulo.
Las medianas
Las medianas se cortan siempre en un punto interior del triángulo.
El baricentro tiene una propiedad física importante: es el centro de gravedad del triángulo.
Si unimos los puntos medios de los lados del triángulo obtenemos el triángulo que tiene el mismo baricentro que y sus medianas miden la mitad que las de .
Además los lados de miden la mitad que los lados de y la superficie de es la cuarta parte de la superficie de , pues podemos comprobar que al trazar se han definido otros tres triángulos iguales: .
Las alturas.
Las alturas de un triángulo acutángulo se cortan siempre en un punto interior del triángulo, luego su orto centro es interior al triángulo.
BIBLIOGRAFIA:
Pendiente & Angulo de inclinación.
http://www.prepafacil.com/cobach/Main/AnguloDeInclinacionYPendienteDeUnaRecta
http://www.slideshare.net/guestcbc7e4/angulos-de-inclinacin-y-pendientes-de-una-recta-111985
Condiciones de paralelismo y perpendicularidad.
http://www.slideshare.net/guestd7dbd4/condiciones-de-paralelismo-y-perpendicularidad
Determinación de la ecuación de la recta.
"
http://educativa.catedu.es/44700165/aula/archivos/repositorio//1750/1987/html/13_determinacin_de_la_ecuacin_de_una_recta.html
Distintas formas de la ecuación de la recta.
http://azul.bnct.ipn.mx/Libros/polilibros/poli11/capitulo2/2.1.htm
Ecuación de la recta en la forma normal.
http://www.acienciasgalilei.com/public/forobb/viewtopic.php?f=4&t=3635
Forma polar de la ecuación de la recta.
http://es.wikipedia.org/wiki/Coordenadas_polares.
Ángulo de intersección entre dos rectas.
http://huitoto.udea.edu.co/Matematicas/4.5.html
Familias de rectas.
. http://geometria-analitica.com/index.php?option=com_content&view=article&id=21&Itemid=31
Aplicaciones de la forma normal de la ecuación de la recta.
http://www.cecytebc.edu.mx/HD/archivos/antologias/geometria_analitica.pdf
Rectas y puntos notables de un triángulo.
http://www.educared.org/wikiEducared/Puntos_y_rectas_notables_de_los_tri%C3%A1ngulos.html
http://www.prepafacil.com/cobach/Main/AnguloDeInclinacionYPendienteDeUnaRecta
http://www.slideshare.net/guestcbc7e4/angulos-de-inclinacin-y-pendientes-de-una-recta-111985
Condiciones de paralelismo y perpendicularidad.
http://www.slideshare.net/guestd7dbd4/condiciones-de-paralelismo-y-perpendicularidad
Determinación de la ecuación de la recta.
"
http://educativa.catedu.es/44700165/aula/archivos/repositorio//1750/1987/html/13_determinacin_de_la_ecuacin_de_una_recta.html
Distintas formas de la ecuación de la recta.
http://azul.bnct.ipn.mx/Libros/polilibros/poli11/capitulo2/2.1.htm
Ecuación de la recta en la forma normal.
http://www.acienciasgalilei.com/public/forobb/viewtopic.php?f=4&t=3635
Forma polar de la ecuación de la recta.
http://es.wikipedia.org/wiki/Coordenadas_polares.
Ángulo de intersección entre dos rectas.
http://huitoto.udea.edu.co/Matematicas/4.5.html
Familias de rectas.
. http://geometria-analitica.com/index.php?option=com_content&view=article&id=21&Itemid=31
Aplicaciones de la forma normal de la ecuación de la recta.
http://www.cecytebc.edu.mx/HD/archivos/antologias/geometria_analitica.pdf
Rectas y puntos notables de un triángulo.
http://www.educared.org/wikiEducared/Puntos_y_rectas_notables_de_los_tri%C3%A1ngulos.html
No hay comentarios:
Publicar un comentario